Menerapkan SM-2 di Rust

Saya telah melakukan tendangan pengulangan spasi (SR) akhir-akhir ini. Mochisoftware SR yang saya gunakan, menggunakan versi modifikasi SuperMemo SM-2 algoritma untuk menjadwalkan kartu. Perbedaannya adalah:

1. Faktor kemudahan (EF) kartu tidak disesuaikan sebagai respons terhadap kinerja, namun dapat diubah secara manual. Pembenarannya adalah hal ini untuk menghindari masalah yang diduga terjadi pada SM-2 yang disebut “meredakan neraka”.
2. Ketika Anda gagal dalam kartu, interval ke tinjauan berikutnya tidak diatur ulang tetapi yang buruk.

Saya tidak suka interval separuhnya, karena kadang-kadang saya akan mengingat sebuah kartu untuk beberapa bulan pertama, lalu melupakannya, dan memasuki keadaan limbo yang aneh ini di mana peninjauan tidak cukup sering bagi saya untuk mempelajari kembali kartu tersebut, jadi saya mulai secara bergantian mengingatnya dan gagal.

Namun saya tidak memahami implikasi perubahan tersebut terhadap faktor kemudahan. Jadi saya memutuskan untuk melihat algoritmanya. Dan, karena apa yang tidak saya buat, saya tidak mengerti, saya menulis implementasi sederhana di Rust.

Tanpa basa-basi lagi, kodenya adalah Di Sini. Berikut penjelasannya.

Mengapa kita membutuhkan algoritma? Kami dapat mengebor setiap kartu setiap hari, tetapi ini akan menjadi mimpi buruk, dan Anda tidak boleh memiliki lebih dari ~200 kartu flash. Penjadwal bertindak sebagai model memori manusia yang sederhana dan kuantitatif. Semakin baik modelnya, semakin besar komitmen kita terhadap memori jangka panjang, dan semakin sedikit waktu yang kita habiskan untuk belajar.

Sebuah barang adalah sepotong pengetahuan yang bersifat atomik, direpresentasikan sebagai kartu flash: pasangan tanya jawab yang menguji keberadaan pengetahuan tersebut. Status suatu item diwakili oleh:

1. Itu faktor pelonggaran $EF$, yang merupakan tingkat kesulitan ganda. Ini adalah bilangan real dalam rentang $(1,3, +infty)$. Nilai awalnya adalah $2,5$.
2. Jumlah pengulangan $n$, yaitu berapa kali kartu ditarik kembali dengan benar secara berturut-turut.

Dari status kartu, kita dapat menghitungnya selang: jumlah hari setelah pengujian terakhir saat item harus ditinjau kembali. Perhitungan interval ditentukan oleh hubungan perulangan dengan jumlah pengulangan:

(begin{align*} I(0) &= 0 \ I(1) &= 1 \ I(2) &= 6 \ I(n) &= I(n-1) kali teks{EF} end{align*})

Ekspresi bentuk tertutupnya adalah:

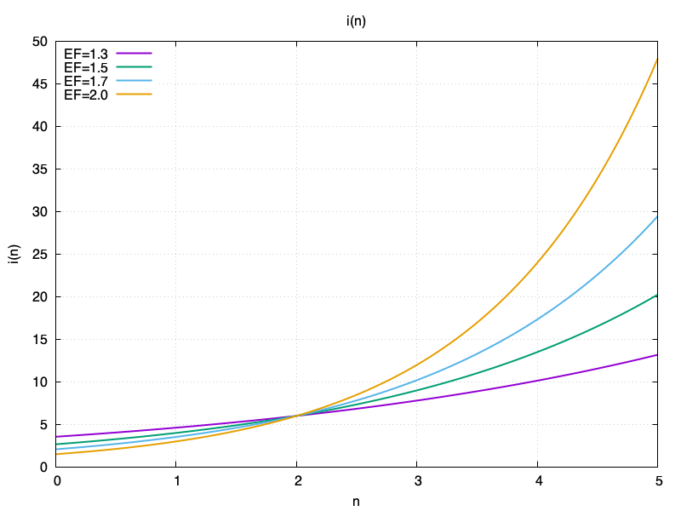
(I(n) = 6 kali text{EF}^{(n-2)})

Sebagai fungsi dari pengulangan yang benar dan EF:

Untuk menguji suatu item, pengguna diperlihatkan pertanyaannya, kemudian mereka mengingat jawabannya secara mental, dan mengungkapkan jawaban sebenarnya. Kemudian pengguna menilai kinerjanya dengan memilih kualitas tanggapan mereka dari daftar ini:

• 0 = Pemadaman listrik. Tidak ada penarikan kembali.
• 1 = Jawaban salah; tapi jawabannya, setelah terungkap, diingat.
• 2 = Jawaban salah; tapi jawabannya sepertinya mudah diingat.
• 3 = Diingat dengan susah payah.
• 4 = Mengingat kembali dengan ragu-ragu.
• 5 = Diingat dengan sempurna.

Nilai kualitas dalam $(0,2)$ mewakili lupa.

Ketika suatu barang diuji, dan kami memiliki kualitas, status barang tersebut harus diperbarui.

Jika pengguna lupa jawabannya, jumlah pengulangan disetel ke nol. Ini berarti intervalnya juga diatur ulang: Anda harus mempelajari kembali kartu tersebut dari awal.

(n'(n, q) = begin{cases} 0 & q in (0,2) \ n+1 & text{otherwise} end{cases})

EF diperbarui dengan menambahkan besaran yang sebanding dengan kualitas respons:

(text{EF}'(text{EF}, q) = min(1.3, text{EF} + f(q)))

Di mana:

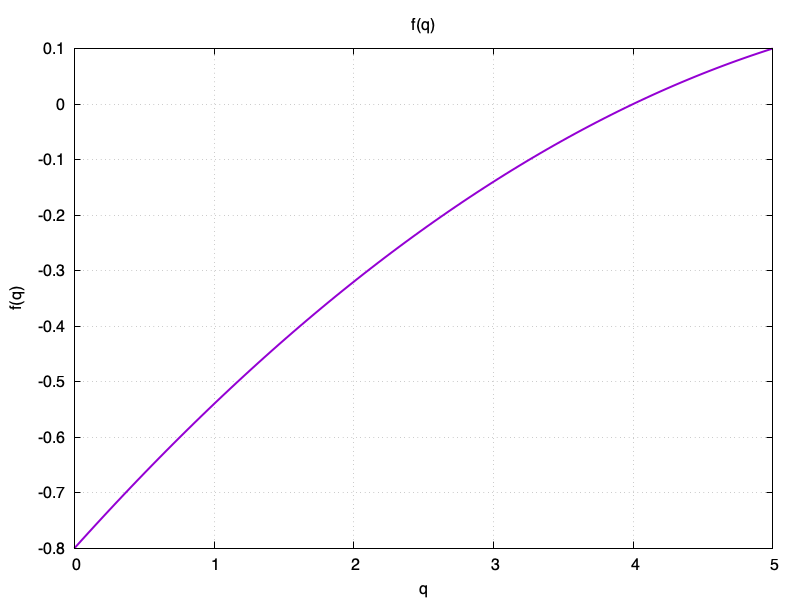
(f(q) = -0,8 + 0,28q – 0,02*q^2)

Secara kualitatif, $f(q)$ terlihat seperti ini:

Jadi untuk recall yang kurang sempurna, EF akan berkurang (sehingga interval berikutnya menjadi lebih pendek), dan hanya recall sempurna yang membuat kartu menjadi lebih mudah. Pada $q=4$ tidak ada perubahan.

Jadi kita merasa sangat mudah: jauh lebih mudah untuk menekan EF ke bawah, atau menjaganya tetap sama, daripada mendorongnya ke atas.

Bagian terakhir dari algoritme ini adalah, di akhir sesi peninjauan, semua item dengan kualitas $(0, 3)$ harus diuji lagi hingga semuanya memiliki kualitas penarikan $(4,5)$.

Jenis skalar:

pub type Repetitions = u32;
pub type Ease = f32;
pub type Interval = u32;

Biasanya saya akan menggunakan tipe baru dengan konstruktor cerdas untuk mewakili tipe dengan rentang (misalnya EF memiliki nilai minimum 1,3). Tapi ini akan membuat kodenya lebih jelek, jadi saya hanya menulis:

pub const INITIAL_EF: Ease = 2.5;
const MIN_EF: Ease = 1.3;

fn min(ef: Ease) -> Ease {
    if ef < MIN_EF {
        MIN_EF
    } else {
        ef
    }
}

Kualitas secara alami direpresentasikan sebagai enum:

#(derive(Debug, Copy, Clone, PartialEq))
pub enum Quality {
    /// Complete blackout.
    Blackout = 0,
    /// Incorrect response; the correct one remembered.
    Incorrect = 1,
    /// Incorrect response; where the correct one seemed easy to recall.
    IncorrectEasy = 2,
    /// Correct response recalled with serious difficulty.
    Hard = 3,
    /// Correct response after a hesitation.
    Good = 4,
    /// Perfect response.
    Perfect = 5,
}

Dengan dua predikat, untuk menguji apakah nilai kualitas ini mengandung arti lupa, dan apakah item tersebut perlu diulang di akhir sesi:

impl Quality {
    pub fn forgot(self) -> bool {
        match self {
            Self::Blackout
            | Self::Incorrect
            | Self::IncorrectEasy => true,
            Self::Hard | Self::Good | Self::Perfect => {
                false
            }
        }
    }

    pub fn repeat(self) -> bool {
        match self {
            Self::Blackout
            | Self::Incorrect
            | Self::IncorrectEasy
            | Self::Hard => true,
            Self::Good | Self::Perfect => false,
        }
    }
}

Status item hanyalah nilai $n$ dan $text{EF}$ (cap waktu tanggal jatuh tempo yang tepat akan diterapkan di luar sistem):

pub struct Item {
    n: Repetitions,
    ef: Ease,
}

Diberikan suatu item, kita dapat menghitung intervalnya:

impl Item {
    pub fn interval(&self) -> Interval {
        let r = self.n;
        let ef = self.ef;
        match self.n {
            0 => 0,
            1 => 1,
            2 => 6,
            _ => {
                let r = r as f32;
                let i = 6.0 * ef.powf(r - 2.0);
                let i = i.ceil();
                i as u32
            }
        }
    }
}

Itu Item::review metode menggunakan item dan, jika diberi peringkat kualitas, memperbarui statusnya:

impl Item {
    pub fn review(self, q: Quality) -> Self {
        Self {
            n: np(self.n, q),
            ef: efp(self.ef, q),
        }
    }
}

Di mana:

fn np(n: Repetitions, q: Quality) -> Repetitions {
    if q.forgot() {
        0
    } else {
        n + 1
    }
}

fn efp(ef: Ease, q: Quality) -> Ease {
    let ef = min(ef);
    let q = (q as u8) as f32;
    let ef = ef - 0.8 + 0.28 * q - 0.02 * q * q;
    min(ef)
}